Figure 1: Our model treats reading of mathematical equation in a document image as generation of textual description which interprets the internal meaning of this equation.

Figure 2: Example of sensitivity of variables, operators and their positions while reading the equations. Only ‘3’ in (a) is changing position in (b), ‘x’ in (a) is changing position in (c), ‘differentiation operator’ in (d) is changed by ‘integration’ in (e), and ‘differentiation operator’ in (d) is changed by ‘finite integration’ in (f), ‘+’ operator in denominator of (g) is changed by ‘−’ in (h), ‘+’ operator in nominator of (g) is changed by ‘−’ in (i), ‘+’ operators in both nominator and denominator of (g) are changed by ‘−’ in (j), variable ‘x’ in (g) is changed by ‘z’ in (k), constant ‘a’ in (g) is changed by ‘b’ in (l), limit value ‘a’ in (g) is replaced by limit value ‘a − ’ in (m), and limit value ‘a’ in (g) is changed to ‘a + ’in (n).

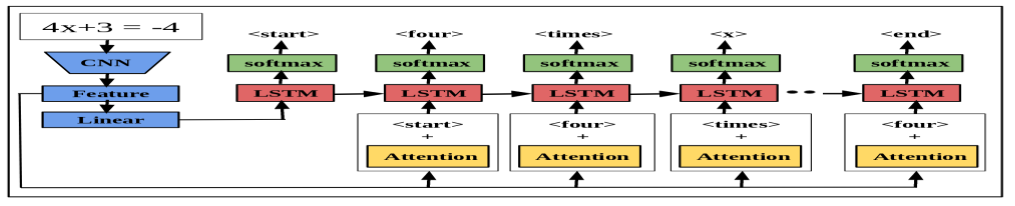
Figure 3: Overview of mathematical expression description network. Our model uses a end-to-end trainable network consisting of CNN followed by a language generating LSTM . It generates textual description of an input mathematical expression image in natural language which interprets its internal meaning.

Table I: Natural language phrases to uniquely describe mathematical equations.

Figure 4: Few sample MEI and their corresponding textual description of Math-Exp-Syn data set.

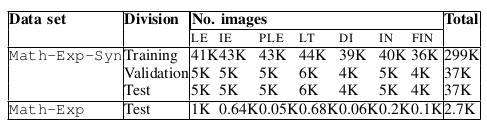
Table II: Category level statistics of considered data sets. LE : linear equation, IE : inequality, PLE : pair of linear equations, LT : limit, DI : differentiation, IN : integral and FIN : finite integral.

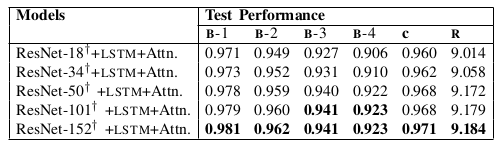
Table III: It illustrates that the deeper pre-trained model gets better representation and improves textual description accuracy with respect to three evaluation measures: BLEU -1 ( B -1), BLEU -2 ( B -2), BLEU -3 ( B -3), BLEU -4 ( B -4), CIDE r ( C ) and ROUGE ( R ) . Number along with the model refers to the depth of the corresponding model. ‘ † ’ denotes that the encoder is fine-tuned during training. LSTM with attention is considered as a decoder.

Table IV: Quantitative illustration of effectiveness of fine- tuning the encoder and attention in decoder during training on MED task. ‘†’ denotes fine-tune.

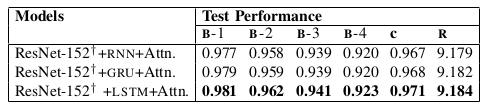
Table V: Performance comparison between RNN , GRU and LSTM with attention mechanism on the mathematical equa- tion description task. We fine-tune the encoder during train- ing process.

Table VI: Quantitative results of our MED model on stan- dard evaluation metrics for both Math-Exp-Syn and Math-Exp data sets. Both the cases MED is trained using training set of Math-Exp-Syn data set.

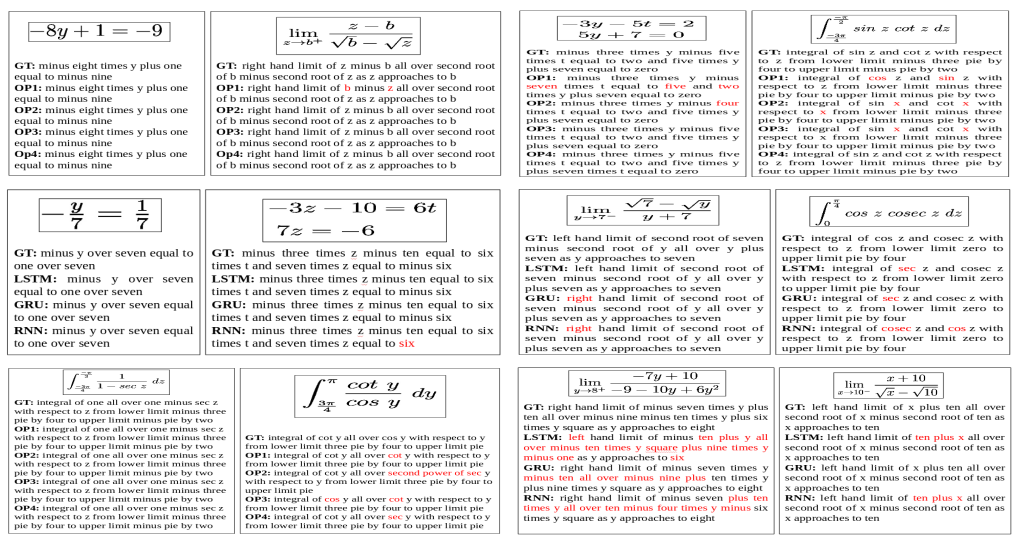
Figure 5: Visual illustration of sample results of test Math-Exp-Syn data set produced by our MED framework. GT : ground truth description, OP 1: description generated by ResNet152+ LSTM , OP 2: description generated by ResNet152+ LSTM +Attn., OP 3: description generated by ResNet152 † + LSTM and OP 4: description generated by ResNet152 † + LSTM +Attn., LSTM : description generated by ResNet152 † + LSTM +Attn., GRU : description generated by ResNet152 † + GRU +Attn., RNN : description generated by ResNet152 † + RNN +Attn., † indicates fine-tune and Attn. denotes attention in decoder. Red colored text indicates wrongly generated text.

Figure 6: Sample cropped mathematical equation images from NCRT class V mathematics book for real world experiment.

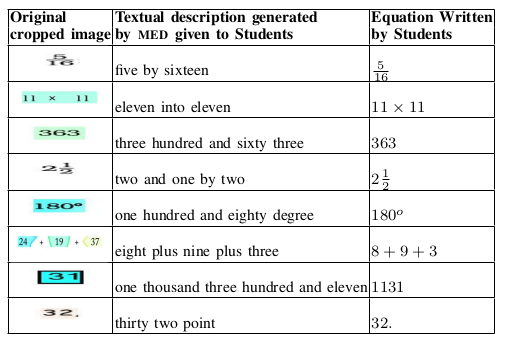
Table VII: Summary of real world experiments. First Column: cropped equation images. Second Column: textual descriptions generated by the MED and given to the students and ask them to write corresponding equations by reading the descriptions. Third Column: equations written by the students.