Image reconstruction on hexagonal lattice
The conventional type of lattice used to define an image is the square lattice. Many existing facts and studies motivated us to explore the possibility of using the hexagonal lattice for generating an upsampled reconstructed image. A regular
hexagonal scheme is optimum for sampling circularly band limited two dimensional signals with least number of required sampling points. Hexagonal sampling requires less number of samples to represent the same information, consequently reducing the storage data space by 13.4%. The hexagonal lattice also offers superior packing efficiency, uniform connectivity, additional equi-distant neighbors and 6-fold rotational symmetry. Due to additional rotational symmetry an image sampled on a hexagonal lattice suffers less interpolation error under rotation as compared to image defined on a square lattice. Reconstruction algorithms implemented using hexagonal lattice have been shown to give images with enhanced quality and to incur reduced computational cost, since hexagonal lattice requires 13 percent less samples than square lattice to represent an image, which matters a lot in the reconstruction world. Hexagonal lattice has been studied and used as an alternative to conventional square lattice for reconstructing the images in tomogprahic world.
PET reconstruction and dictionary based denoising
PET is a nuclear imaging modality used to study functional activities of living tissues such as glucose metabolism etc. It is an emission modality which is invasive in the sense that it involves injection of positron emitting radio-isotopes into the patient. The injected radio-isotope decays during its metabolism inside the tissues, emitting positrons. These positrons annihilate after colliding with their anti-particle, electron. The γ-photons emitted as result travel in radially opposite directions which are detected outside the body by the PET scanner. The emitted photons (each of energy 511 KeV) however interact with body tissue in their ideal straight line path. Compton scattering is one of the most prominent interaction that the photons undergo. These interactions lead to photons losing some energy as well as changing their direction. This scattering effect leads to ‘attenuation’ of photons, which is the major cause of degradation in PET images.
The attenuation correction factors for PET are estimated using external photon sources with the body present and comparing it with ones without any body present in the scanner. In addition to the attenuation correction, sinogram also needs to be corrected for noise arising from scatter(due to interaction of photons with body) and random events such as other positrons annihilating at the same time. In this work, we do not attempt to correct this error or the errors which arise due to non-uniformity of detectors of PET scanner. The proposed pipeline for denoising has two stages: In stage 1, the PET image is reconstructed onto a desired lattice from the given sinogram and in stage 2 the reconstructed image is denoised using the KSVD algorithm.
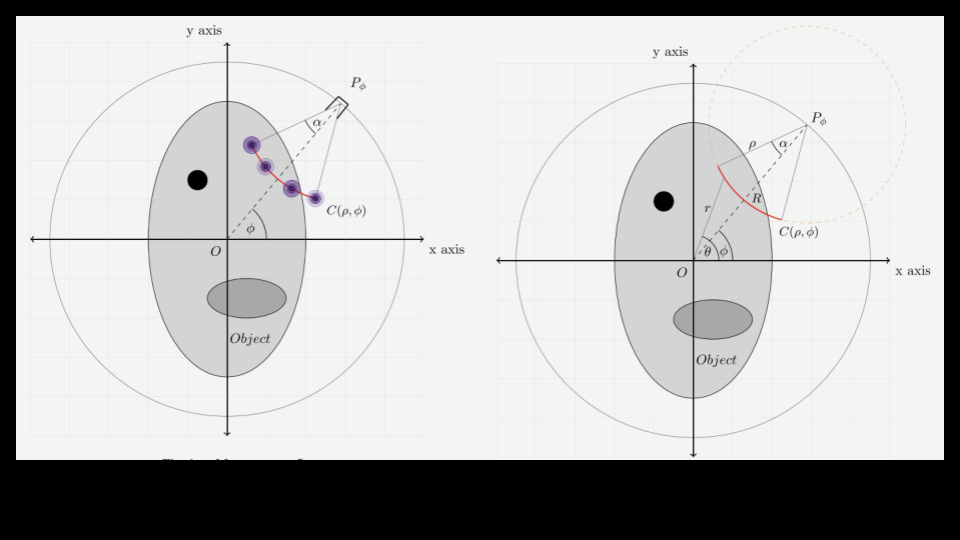
Numerical inversion of circular arc Radon transform
Circular arc Radon (CAR) transforms associate to a function, its integrals along arcs of circles. The inversion of such transforms is of natural interest in several imaging modalities such as thermoacoustic and photoacoustic tomography, ultrasound and intravascular imaging. Unlike the full circle counterpart – the circular Radon transform – which has attracted significant attention in recent years, the CAR transforms are scarcely studied objects. In this work, we presented an efficient algorithm for the numerical inversion of the CAR transform with fixed angular span, for the cases in which the support of the function lies entirely inside or outside the acquisition circle. The numerical algorithm is non-iterative and is very efficient as the entire scheme, once processed, can be stored and used repeatedly for reconstruction of images. A modified numerical inversion algorithm is also proposed to reduce the artifacts in the reconstructed image which are induced due to the limited angular span.
Artifact supression in numerical reconstructed images
In the classical setting of the tomographic reconstruction problem, the tomographic data (= Rf(φ, ρ)) is assumed to be known for all values (φ, ρ) ∈ S1 × R. This tomographic problem has been extensively studied in both linear as well as circular case and reconstruction algorithms are available for complete data. However, in the present work we consider data which is limited in both φ as sell as ρ variable, i.e tomographic data is not available for the whole S1 × R. This limited data scenario introduces singularities in the acquired data due to hard cut off of the data. These singularities in the data manifest in the form of artifacts in the reconstructed image. A framework for analysing and handling artifacts has been provied. The framework provides a general approach for analysing the artifacts in computed tomography. We analysed, numerically, the effect of various parameters on the artifacts in the reconstructed image. Further, we proposed an artifact suppression strategy for the Circular arc Radon transform.