Real Time Rendering of Implicit Surfaces on the GPU

Jag Mohan Singh

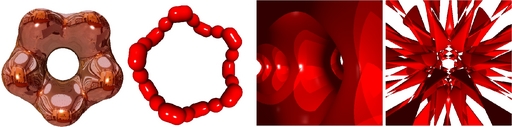
Generating visually realistic looking models is one of the core problems of Computer Graphics. Rasterization or scan converting the primitives used such as triangles is one method to render them. This method suffers from problems of an inexact representation as triangles themselves are an approximation of the underlying geometry. Ray tracing primitives is another method of rendering the objects. This method delivers exact representation of the underlying geometry and looks visually realistic. We thus use ray tracing of implicit surfaces rather than polygonizing them. The programmable graphics processor units (GPUs) have high computation capabilities but relatively limited bandwidth for data access. Compact representation of geometry using a suitable procedural or mathematical model and a ray-tracing mode of rendering fit the GPUs well, consequently. An implicit surface can be represented as S(x,y,z) = 0 and the ray dependent equation is F_f(t) = 0. Ray tracing S(x,y,z) = 0 is root computation of F_f(t) = 0 for all the pixels on the screen. Analytical methods can be used in surfaces up to order 4. We compute interval extension of functions exactly by computing the function at points of maxima and minima and end points. Since, we can compute roots of functions up to order 4 we can compute points of maxima and minima of functions up to order 5. We use interval arithmetic for surfaces up to order 5 using Mitchell's algorithm. Interval methods provide a robust way for root isolation. Marching points algorithm marches in equal stepsizes until the root is found which is detected by a sign change in the function. Marching points wastes computation by computing the function values at many points. Adaptive marching points algorithm marches adaptively to find the root. Though only fourth or lower order surfaces can be rendered using analytical roots, our adaptive marching points algorithm can ray-trace arbitrary implicit surfaces exactly, by sampling the ray at selected points till a root is found. Adapting the sampling step size based on a proximity measure and a horizon measure delivers high speed. The horizon measure helps in silhouette adaptation and provides good quality silhouettes. We also provide a taylor test which has flavours of interval arithmetic and helps in robust rendering of surfaces using adaptive marching points algorithm. While computing the function S(x,y,z) = 0 we never compute the ray dependent F_f(t) = 0 by using coefficients of t. We save lot of computational overhead by computing S(x,y,z) = 0 directly instead as there are O(d^3) coefficients for t where d is the degree of the surface. In our method we don't need coefficients of t which are expensive to compute we only need the value S(x,y,z) = 0. The derivative F'_f(t) can also be calculated efficiently using the gradient of S() as grad(S(x, y, z)) dot D_f. The Barth decic can be evaluated using about 30 terms as S(x, y,z) but needs to evaluate 1373 terms to compute all 11 coefficients of the tenth order polynomial F_f(t). We render Dynamic Implicit Surfaces which vary with time. Overall, a simple algorithm that fits the SIMD architecture of the GPU results in high performance. We ray-trace algebraic surfaces up to order 18 and non-algebraic surfaces including a Blinn's blobby with 30 spheres at better than interactive frame rates. Our adaptive marching points is an ideal match for the SIMD model of GPU due to low computational cost required per operation. We use analytical methods for ray tracing surfaces up to order 4. We achieve fps of 3750 on a cubic surface and 1400 on a quartic surface. We use the robust Mitchell method on surfaces up to order 5 and achieve fps up to 400 on a torus quartic and 85 on a quintic surface. Our adaptive marching points method renders high order implicit surfaces at interactive frame rates. We render surface of order 18 at an fps of 158. These experiments used NVIDIA 8800 GTX at a resolution of 512x512. Our GPU Objects renders Bunny with 35,947 spheres at 57 fps, 99,130 spheres is rendered at 30 fps and Hyperboloid with reflection and refraction at 300 fps. NVIDIA 6600 GTX was used in experiments related to GPU Objects and the viewport was of the size 512x512.

Related Publications

• Jag Mohan Singh and P. J. Narayanan - Real-Time Ray Tracing of Implicit Surfaces on the GPU IEEE Transactions Visualization and Computer Graphics, Vol. 16(2), pp. 261-272 (2010). [PDF]

• Visesh Chari,  Jag Mohan Singh and P. J. Narayanan - Augmented Reality using Over-Segmentation Proceedings of National Conference on Computer Vision Pattern Recognition Image Processing and Graphics (NCVPRIPG'08),Jan 11-13, 2008, DA-IICT, Gandhinagar, India. [PDF]
  

• Kedarnath Thangudu, Lakshmi Gade, Jag Mohan Singh and P. J. Narayanan - Point Based Representations for Hierarchical Environments In International Conference on computing: Theory and Applications(ICCTA), Kolkatta, 2007. [PDF]

• Jag Mohan Singh and P.J. Narayanan - Progressive Decomposition of Point Clouds Without Local Planes, 5th Indian Conference on Computer Vision, Graphics and Image Processing, Madurai, India, LNCS 4338 pp.364-375, 2006. [PDF]
  

• Sunil Mohan Ranta, Jag Mohan singh and P.J. Narayanan - GPU Objects , 5th Indian Conference on Computer Vision, Graphics and Image Processing, Madurai, India, LNCS 4338 pp.352-363, 2006. [PDF]

Downloads