Projected Texture for 3D Object Recognition

Introductiondeformation geometry

Three dimensional object are characterized by their shape, which can be thought of as the variation in depth over the object, from a particular view point. These variations could be deterministic as in the case of rigid objects or stochastic for surfaces containing a 3D texture. These depth variations are lost during the process of imaging and what remains is the intensity variations that are induced by the shape and lighting, as well as focus variations. Algorithms that utilize 3D shape for classification tries to recover the lost 3D information from the intensity or focus variations or using additional cues from multiple images, structured lighting, etc. This process is computationally intensive and error prone. Once the depth information is estimated, one needs to characterize the object using shape descriptors for the purpose of classification.

Image-based classification algorithms tries to characterize the intensity variations of the image of the object for recognition. As we noted, the intensity variations are affected by the illumination and pose of the object. The attempt of such algorithms is to derive descriptors that are invariant to the changes in lighting and pose. Although image based classification algorithms are more efficient and robust, their classification power is limited as the 3D information is lost during the imaging process.

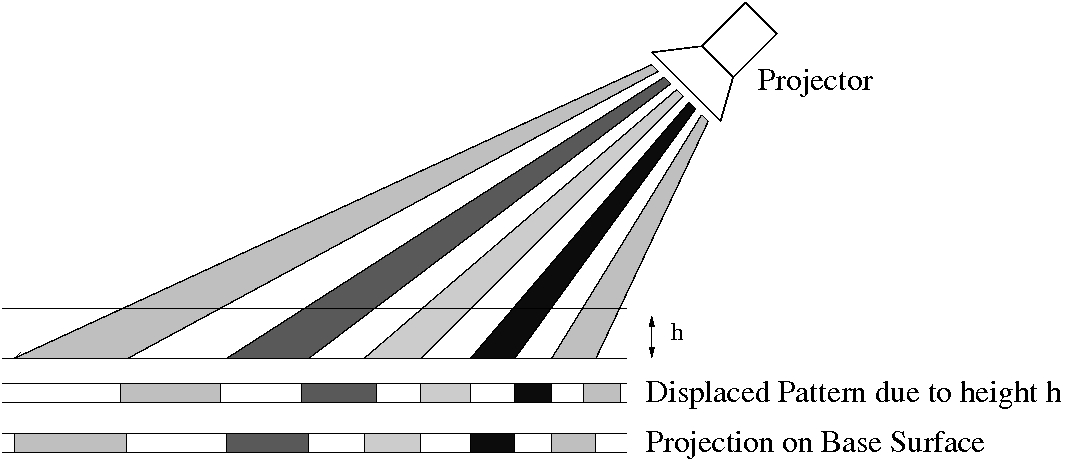pattern shift1We propose the use of structured lighting patterns, which we refer to as projected texture, for the purpose of object recognition. The depth variations of the object induces deformations in the projected texture, and these deformations encode the shape information. The primary idea is to view the deformation pattern as a characteristic property of the object and use it directly for classification instead of trying to recover the shape explicitly. To achieve this we need to use an appropriate projection pattern and derive features that sufficiently characterize the deformations. The patterns required could be quite different depending on the nature of object shape and its variation across objects.

 

 

feat
 saltSugar

3D Texture Classification

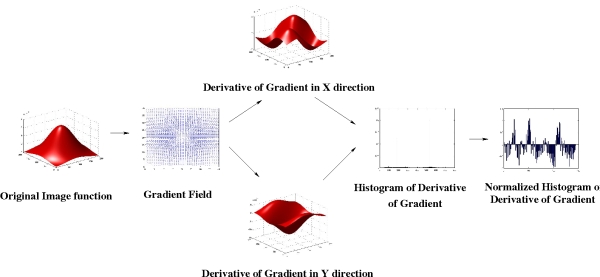
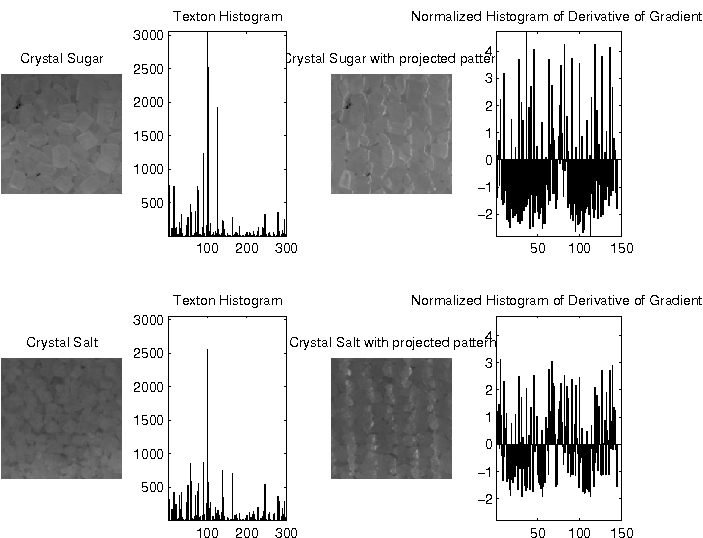
A feature "Normalized Histogram of Derivative of Gradients (NHoGD) is proposed to capture deformation statistic for parallel projection patterns.

Gradient directions in images are the directions of maximal intensity variation. In our scenario, the gradient directions can indicate the direction of the projected lines. As the lines get deformed with surface height variations, we compute the differential of the gradient directions in both x and y axes to measure the rate at which the surface height varies. The derivatives of gradients are computed at each pixel in the image, and the texture is characterized by a Histogram of the Derivatives of Gradients (HoDG). The gradient derivative histogram is a good indicator of the nature of surface undulations in a 3D texture. For classification, we treat the histogram as a feature vector to compare two 3D textures. As the distance computation involves comparing corresponding bins from different images, we normalize the counts in each bin of the histogram across all the samples in the training set. This normalization allows us to treat the distance between corresponding bins between histograms, equally, and hence employ the Euclidean distance for comparison of histograms. The Normalized histograms, or NHoDG is a simple but extremely effective feature for discriminating between different texture classes. Figure on right illustrates the computation of the NHoDG feature from a simple image with bell shaped intensity variation.

 

 

 

imgCategory Recognition for Rigid Objects

The primary concerns in developing a representation for object category is that the description should be invariant to both shape and pose of the object. Note that the use of projected patterns allows us to avoid object texture, and concentrate only on its shape. Approaches such as ’bag of words’ computed from interest points have been successfully employed for image based object category recognition.

Our approach is similar in spirit to achieve pose invariance. We learn the class of local deformations that are possible for each category of objects by creating a codebook of such deformations from a training set. Each object is then represented as a histogram of local deformations based on the codebook. Figure on left illustrates the computation of the feature vector from a scene with projected texture. There are two primary concerns to be addressed while developing a parts based shape representation: The location of points from which the local shape descriptor is computed is important to achieve position invariance. In image based algorithms, the patches are localized by using an interest operator that is computed from object texture or edges. However, in our case the primary objective is to avoid using texture information and concentrate on the shape information provided by the projected texture. Hence we choose to use a set of overlapping windows that covers the whole scene for computation of local deformations. Our representation based on the codebook allows us to concentrate on the object deformation for recognition. The description of the local deformations should be sufficient to distinguish between various local surface shapes within the class of objects. The feature vector used exploits the periodic nature of projected patterns. Since Fourier representation is an effective descriptor for periodic signals, and since we are interested in the nature of deformation and not its exact location, we compute magnitude or the absolute value of the Fourier coefficients (AFC) corresponding to each of the window patch as our feature vector. To make comparisons in a Euclidean space for effective, we use a logarithmic representation of these coefficients (LAFC). We show that this simple Fourier magnitude based representation of the patches can effectively achieve the discriminative power that we seek. The feature extraction process proceeds as follows: The images in the training set are divided into a set of overlapping windows of size 20×20 (decided experimentally). Each window is then represented using the magnitude of Fourier representation in logarithmic scale. This results in a 200 dimensional feature vector (due to symmetry of Fourier representation) for each window. A K-means clustering of windows in this feature space allows us to identify the dominant pattern deformations, which forms a codebook

comparison1

Recognition of Aligned Deterministic shapes

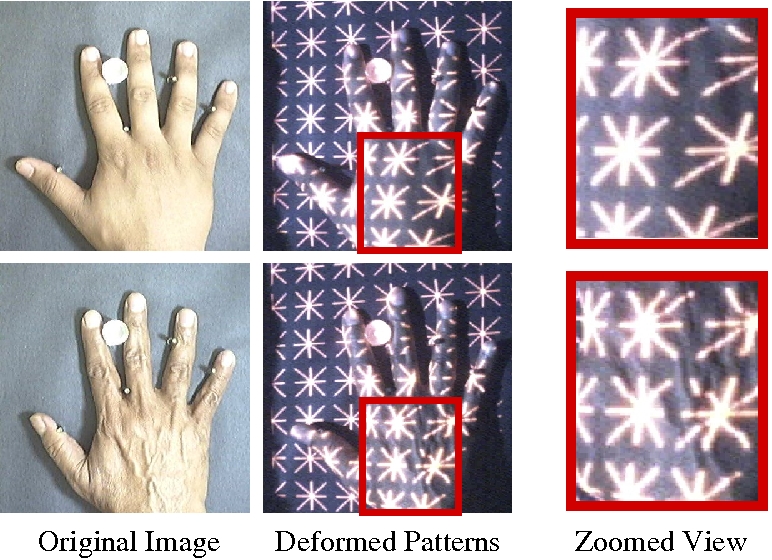
We have taken the example of hand geometry based person authentication for demonstrating our approach. We have collected dataset of 181 user with peg based alignment. We divided the hand image into a set of non-overlapping sub-windows, and compute the local textural characteristics of each window using a filter bank of 24 Gabor filters with 8 orientations and 3 scales (or frequencies).

Related Publications

  • Avinash Sharma, Nishant Shobhit and Anoop M. Namboodiri - Projected Texture for Hand Geometry based Authentication Proceedings of CVPR Workshop on Biometrics, 28 June, Anchorage, Alaska, USA. IEEE Computer Society 2008. [PDF]

 

  • Avinash Sharma, Anoop Namboodiri - Projected Texture for classification of 3D Texture Surface, Submitted to ECCV 2008 (Results awaited)
  • Avinash Sharma, Anoop Namboodiri - Object Category Recognition with Projected Texture, Submitted to ICPR 2008 (Results awaited)

  • Avinash Sharma - A Technical Report on Projected Texture for Object Recognition

Associated People