Topological Mapping for Manhattan-like Repetitive Environments
Abstract
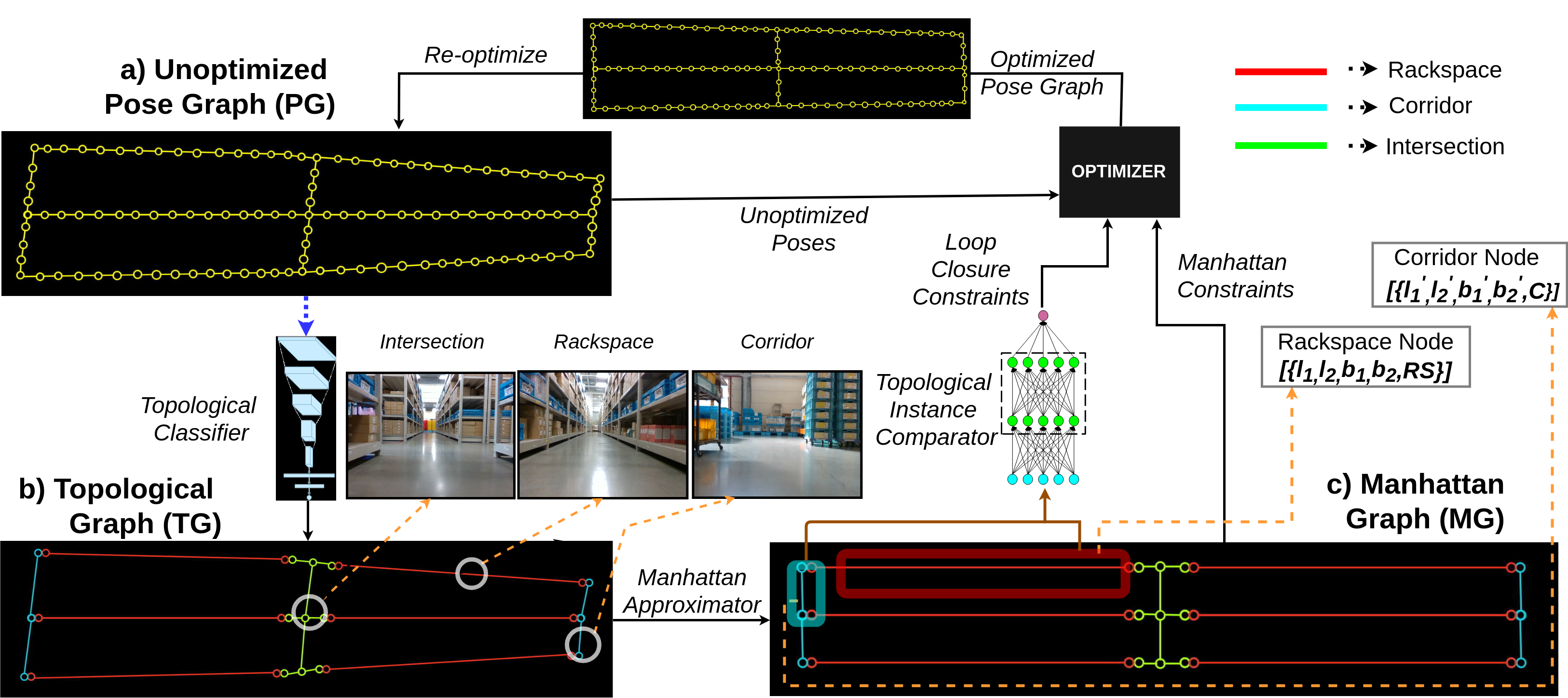
We showcase a topological mapping frameworkfor a challenging indoor warehouse setting. At the most abstractlevel, the warehouse is represented as a Topological Graphwhere the nodes of the graph represent a particular warehousetopological construct (e.g. rackspace, corridor) and the edgesdenote the existence of a path between two neighbouringnodes or topologies. At the intermediate level, the map isrepresented as a Manhattan Graph where the nodes and edgesare characterized by Manhattan properties and as a Pose Graphat the lower-most level of detail. The topological constructsare learned via a Deep Convolutional Network while therelational properties between topological instances are learntvia a Siamese-style Neural Network. In the paper, we showthat maintaining abstractions such as Topological Graph andManhattan Graph help in recovering an accurate Pose Graphstarting from a highly erroneous and unoptimized Pose Graph.We show how this is achieved by embedding topological andManhattan relations as well as Manhattan Graph aided loopclosure relations as constraints in the backend Pose Graphoptimization framework. The recovery of near ground-truthPose Graph on real-world indoor warehouse scenes vindicatethe efficacy of the proposed framework.
Introduction
We showcase a topological mapping framework for a challenging indoor warehouse setting. At the most abstract level, the warehouse is represented as a Topological Graph where the nodes of the graph represent a particular warehouse topological construct (e.g. rackspace, corridor) and the edges denote the existence of a path between two neighbouring nodes or topologies. At the intermediate level, the map is represented as a Manhattan Graph where the nodes and edges are characterized by Manhattan properties and as a Pose Graph at the lower-most level of detail. The topological constructs are learned via a Deep Convolutional Network while the relational properties between topological instances are learnt via a Siamese-style Neural Network. In the paper, we show that maintaining abstractions such as Topological Graph and Manhattan Graph help in recovering an accurate Pose Graph starting from a highly erroneous and unoptimized Pose Graph. We show how this is achieved by embedding topological and Manhattan relations as well as Manhattan Graph aided loop closure relations as constraints in the backend Pose Graph optimization framework. The recovery of near ground-truth Pose Graph on real-world indoor warehouse scenes vindicate the efficacy of the proposed framework.
Qualitative Results:
1)RTABMAP SLAM
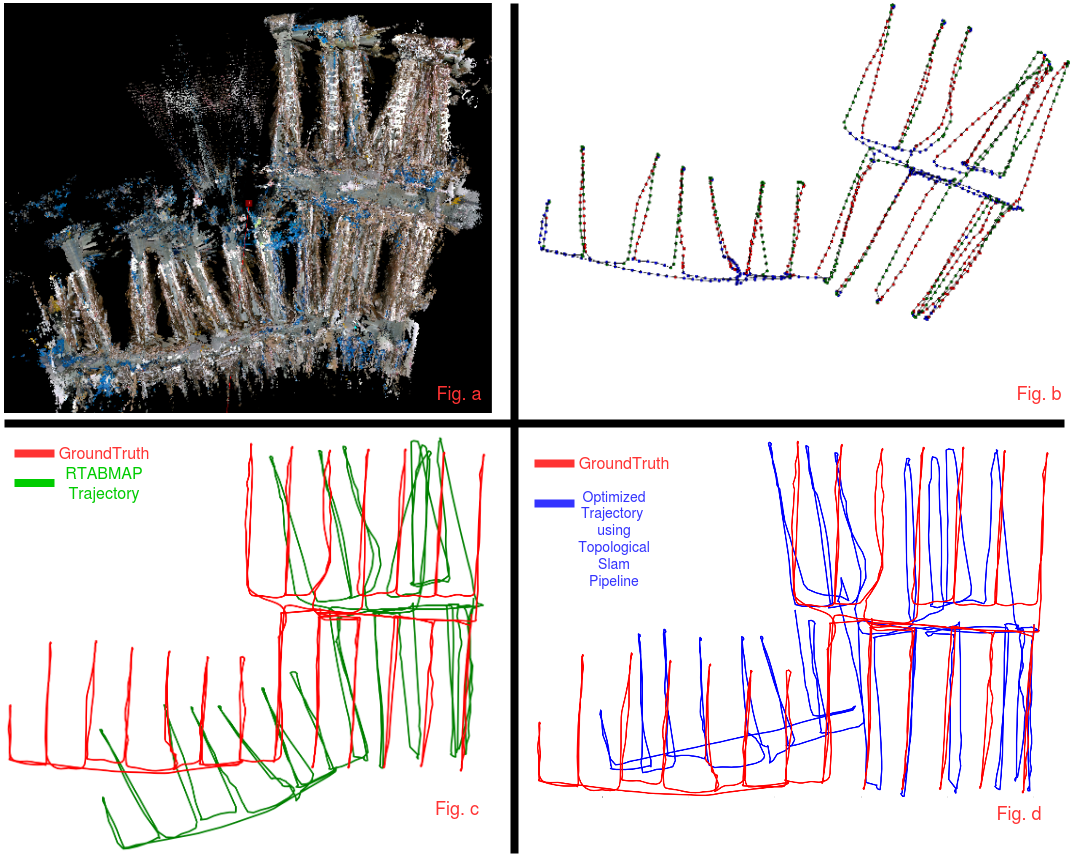
Fig. a shows registered map generated by RTABMAP Slam. Fig. b shows RTABMAP trajectory with topological labels. Fig. c compares the RTABMAP trajectory with groundtruth trajectory. Fig. d compares trajectory generated using our topological SLAM pipeline with groundtruth.
2)RTABMAP as Visual Odometry pipeline
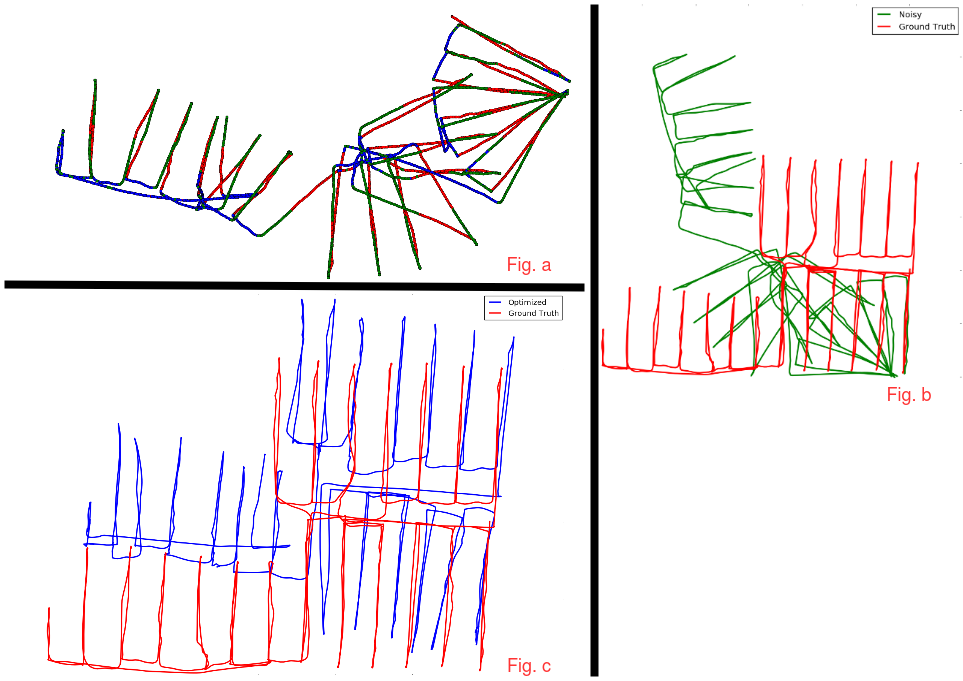
Fig. a shows trajectory obtained using RTABMAP with loop closure turn off. Wheel odometry is used as odometry source. Fig. b compares RTABMAP trajectory with groundtruth. Fig. c compares trajectory obtained using Topological Slam pipeline with groundtruth.


Code:
Our pipeline consists of 3 parts - each sub-folder in this repo containts code for each:
- Topological categorization using a convolutional neural network classifier -> Topological Classifier
- Predicting loop closure constraints using Multi-Layer Perceptron -> Instance Comparator
- Graph construction and pose graph optimization using obtained Manhattan and Loop Closure Constraints -> Pose Graph Optimizer
How to use each is explained in corresponding sub-folder
Please find GitHub Project Page
Bibtex
If you find our work useful in your research, please consider citing:
@article{ puligilla2020topo,
author = { Puligilla, Sai Shubodh and Tourani, Satyajit and Vaidya, Tushar and Singh Parihar, Udit and Sarvadevabhatla, Ravi Kiran and Krishna, Madhava },
title = { Topological Mapping for Manhattan-Like Repetitive Environments },
journal = { ICRA },
year = { 2020 },
}
