Histo Pathological Image Analysis

Automated analysis of histo-pathological images is attracting much interest in the recent past .Most of these images are largely characterised by colour, textural and morphological features and not gross anatomical structures found in radiology (neuroimages, lung,CT etc). A fundamental task in CAD tool development for histopathological images is detection and segmentation of structures such as lymphocytes, nuclei, stroma, etc.

In regards to histopathological image analysis, we are currently working on mitosis detection in H & E stained breast biopsy slides .Mitosis detection and quantification is a key task in grading of cancer. In designing a pipeline for the detection problem, identification of stroma in the tissue is important when comes to rejection of false candidates.

People Involved

• Anisha

Retinal Image Analysis

Retinal images are widely used for dignostic purposes by opthalmologists. They provide vital information about the health of the sensory part of the visual system.

Several diseases that can lead to blindness manifest as artifacts in the retinal image. Automatic segmentation and analysis of retinal images can therefore be used to diagnose these diseases.

Our current work focuses on following areas:

• General Segmentation
• Uni-modal and cross-modal registration
• Disease Analysis
• Content Based Image Retrieval (CBIR) of Retinal Images

General Segmentation - Developing techniques for segmenting various structures of interest such as blood vessel tree, optic disk and the macula within the retina.

Uni-modal and cross-modal registration Developing techniques for retinal image registration in order to combine the complementary information in different and same retinal image modalities image.

Disease Analysis - Developing techniques for identifying, quantifying and tracking signs of different types of diseases.

Some of the projects in disease analysis are :

• Detection and quantification of lesions that occur at very early stages of Diabetic Retinopathy (DR). Examples of such lesions are microaneurysms and hard exudates. The aim is to detect these from color fundus images as it is of prime importance in developing solutions for screening programmes among large populations.
• Detection of Capillary non-perfusion (CNP), which occurs in advanced stages of DR. The aim is to detect and quantify the total area covered by these lesions from FFA images.
• Detection, counting and grading of drusen, that occur due to Age-related macular degeneration(AMD)

Our current collaborators are: LVPEI, Aravind Eye Institute, Hyderabad and Aravind Eye Hospital, Madurai.

Content Based Image Retrieval (CBIR) of Retinal Images

Image search through Content Based Image Retrieval (CBIR) is a challenging problem in a large database. This becomes more complex in medical images as the interest for retrieval is based on semantics (pathology/anatomy) rather than just the visual similarity.

We are currently working on devising a CBIR solution for retinal images in the ophthalmology department of hospitals. By applying CBIR in medical image databases we aim to assist ophthalmologists and students for teaching and self training on the computer. This is based on the assumption that visual characteristics of a disease carry diagnostic information and often visually similar images correspond to the same disease category. 

People Involved

• Arunava Chakravarty
• Ujjwal
• Gopal
• Akhilesh
• Sai
• Yogesh

Retinal Image Datasets

Our Datasets

- Capillary Nonperfusion (CNP) Analysis Dataset *
- Age-related Macular Degeneration (AMD) Analysis Dataset *
- Optic Nerve Head (ONH) segmentation Dataset (Drishiti-GS 1)

* - available on request

Other Available Datasets

- Digital Retinal Images for Vessel Extraction (DRIVE)
- STructured Analysis of the Retina (STARE)
- Standard Diabetic Retinopathy Database (DIARETDB0 & DIARETDB1)
- Methods to evaluate segmentation and indexing techniques (MESSIDOR)
- Test suite of 18 challenging pairs of images for testing registration algorithms
- Image Database and Archive (RISA)
- Collection of multispectral images of the fundus

Other Retinal Image Analysis Groups

- Department of computer Science, University of Bristol
- IMAGERET
- MESSIDOR
- Retinal Image Analysis Group: Columbia University
- Retinopathy image search and analysis (RISA)
- Structured Analysis of the Retina (STARE)
- DRIVE : Digital Retinal Images for Vessel Extraction

Reading References

- Online Retinal Image Analysis Reference

Retinal Image Tools

* Available Soon

Events

• Retinopathy Online Challenge (ROC) is underway
• DIARETDB released
• Selected conferences in the field of Medical Imaging
• Medical Image Analysis Journals and Conference Proceedings
• Conferences Computer Vision, Image Processing and Medical Image Analysis
• Medical Imaging Computing
• European Society of Retina Specialists (EURETINA)
• Digital Healthcare Conference
• The International Diabetes Federation (IDF)

Semantic Classification of Boundaries of an RGBD Image

Nishit Soni, Anoop M. Namboodiri, CV Jawahar and Srikumar Ramalingam. Semantic Classification of Boundaries of an RGBD Image. In Proceedings of the British Machine Vision Conference (BMVC 2015), pages 114.1-114.12. BMVA Press, September 2015. [paper] [abstract] [poster] [code] [bibtex]

Download the dataset from here.

Summary

Edges in an image often correspond to depth discontinuities at object boundaries (occlusion edges) or normal discontinuities (convex or concave edges). In addition, there could be planar edges that are within planar regions. Planar edges may result from shadows, reflection, specularities and albedo variations. Figure 2 shows a sample image with edge labels. Figure 1 represents the kinect depth map of that image. This paper studies the problem of classifying boundaries from RGBD data. We propose a novel algorithm using random forest for classifying edges into convex, concave and occluding entities. We release a data set with more than 500 RGBD images with pixel-wise groundtruth labels. Our method produces promising results and achieves an F-score of 0.84.

We use both image and depth cues to infer the labels of edge pixels. We start with a set of edge pixels obtained from an edge detection algorithm and the goal is to assign one of the four labels to each of these edge pixels. Each edge pixel is uniquely mapped to one of the contour segments. Contour segments are sets of linked edge pixels. We formulate the problem as an optimization on a graph constructed using contour segments. We obtain unary features using pixel classifier based on Random forest. We design a feature vector with simple geometric depth comparison features. We use a simple Potts model for pairwise potentials. The individual steps in the algorithm is shown in figure 3.

Figure 3 : This figure summarizes the pipeline of our approach. It shows RGB and depth maps as input (1st image set), with Pb edge detection (2nd image). The classification and MRF outputs are shown in the last two images respectively. Color code: red (occluding), green (planar), blue (convex), yellow (concave).

Experiments and Results

For quantitative evaluation of the method, we have created an annotated dataset of 500 RGBD images of varying complexity. Train to test ratio is 3:2. Our dataset consists of objects such as tables, chairs, cupboard shelves, boxes and household objects in addition to walls and floors. We also annotate 100 images from NYU dataset, which include varying scenes from bed-room, living-room, kitchen, bathroom and so on with different complexities.

We compare our approach with Gupta et al. [1] and show that our approach provides better results. The approach that we present here provides good labels for most pixels with high precision and the performance degrades when there is a significant loss in the depth data. We get an average F-score of 0.82 on the classification results for our data set. The use of smoothness constraints in the MRF achieves an F-score of 0.84. The NYU dataset contains complex scenes containing glass windows and table heads. We achieve an average F-score of 0.74 for the NYU dataset. Below is the quantitative evaluation of our approach along with the comparison with Gupta et al..

Results on NYU dataset (click to enlarge)
Color code: red (occluding), green (planar), blue (convex), yellow (concave)

Groundtruth
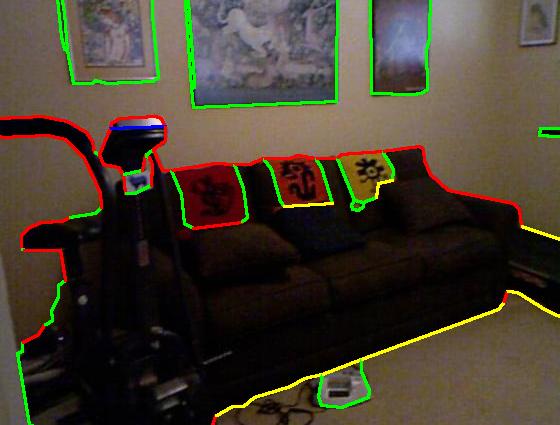Result

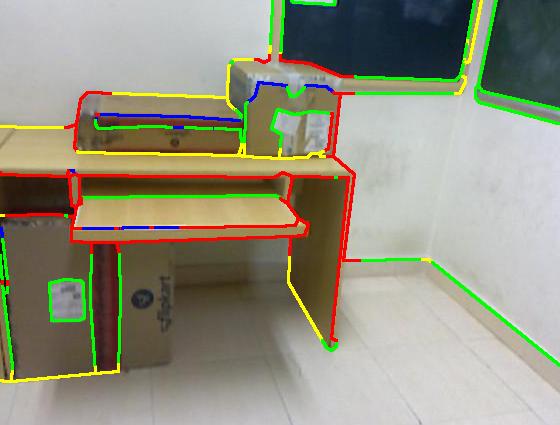
Results on our dataset (click to enlarge)
Color code: red (occluding), green (planar), blue (convex), yellow (concave)

Groundtruth
Our result
Sgupta et al. [1]

References 

1. S. Gupta, P. Arbelaez, and J. Malik. Perceptual organization and recognition of indoor scenes from rgb-d images. In CVPR, 2013.

Authors

Nishit Soni ¹
This email address is being protected from spambots. You need JavaScript enabled to view it.

Anoop M. Namboodiri ¹
This email address is being protected from spambots. You need JavaScript enabled to view it.

C. V. Jawahar ¹
This email address is being protected from spambots. You need JavaScript enabled to view it.

Srikumar Ramalingam ²
This email address is being protected from spambots. You need JavaScript enabled to view it.

¹ International Institute of Information Technology, Hyderabad.
² Mitsubishi Electric Research Lab (MERL), Cambridge, USA.

Parallel Computing using CPU and GPU

Introduction

Commodity graphics hardware has become a cost-effective parallel platform to solve many general problems; owing to its low cost to performance ratio (under $0.5 per GFLOP). GPUs are optimized for graphics operations and their programming model is highly restrictive. All algorithms are disguised as graphics rendering passes with the programmable shaders interpreting the data. This was the situation until the latest model of GPUs following the Shader Model 4.0 were released late in 2006. These GPUs follow a unified architecture and can be used in more flexible ways than their predecessors. Starting from the G80 series of GPUs, Nvidia offers an alternate programming model called Compute Unified Device Architecture (CUDA) to the underlying parallel processor. CUDA is highly suited for general purpose programming on the GPUs and provides a model close to the PRAM model. There has been a tremendous amount of growth in both the programmability and efficiency of GPUs over the years, leading to many GPU based solutions for general purpose problems.

Projects involving GPU's and CUDA

1. String Sort on GPUs

String sorting or variable-length key sorting has lagged in performance on the GPU even as the fixed-length key sorting has improved dramatically. Radix sorting is the fastest on the GPUs. In this work, we present a fast and efficient string sort on the GPU that is built on the available radix sort. Over 70% of the string sort time is spent on standard Thrust primitives for sort, scatter and scan. This provides high performance along with high adaptability to future GPUs. Our string sort algorithm is 10x faster compared to current GPU methods.

2. Mixed-Resolution Patch Matching

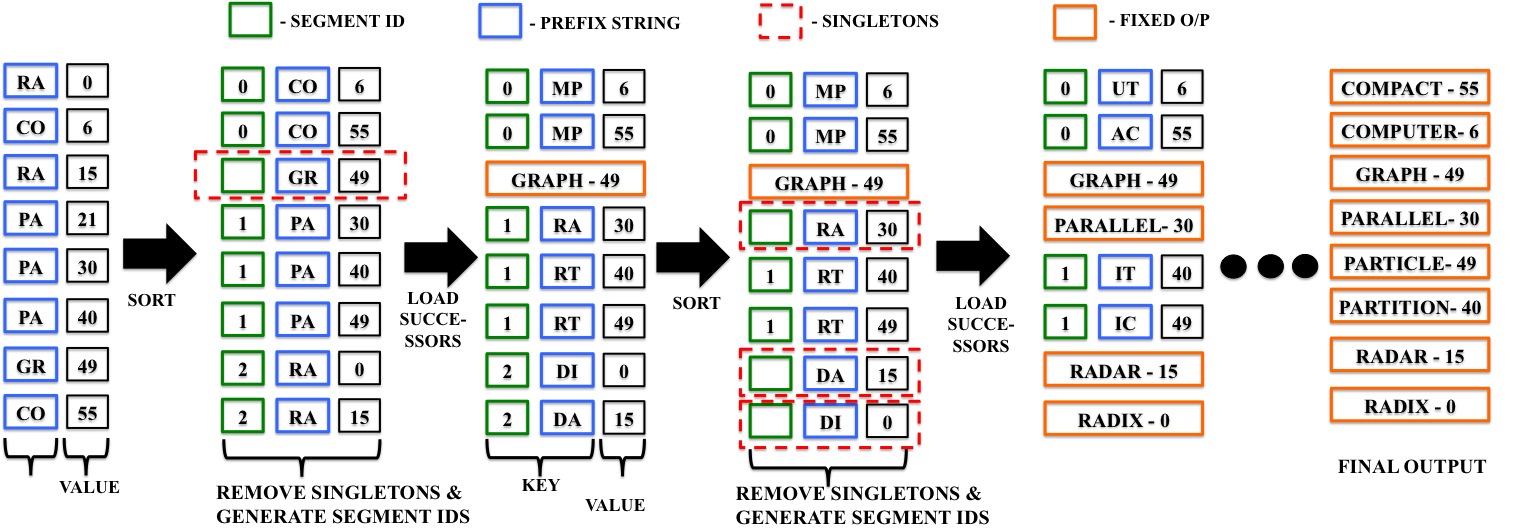
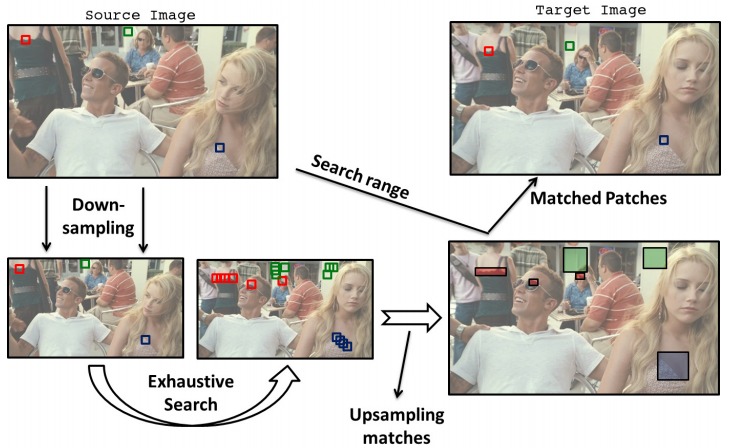Matching patches of a source image with patches of itself or a target image is a first step for many operations. Finding the optimum nearest-neighbors of each patch using a global search of the image is expensive. Optimality is often sacrificed for speed as a result. In this work, we developed the Mixed-Resolution Patch-Matching (MRPM) algorithm that uses a pyramid representation to perform fast global search. We compare mixed-resolution patches at coarser pyramid levels to alleviate the effects of smoothing. We store more matches at coarser resolutions to ensure wider search ranges and better accuracy at finer levels. Our method achieves near optimality in terms of exhaustive search. Our simple approach enables fast parallel implementations on the GPU, yielding upto 70x speedup compared to other iterative approaches.

3. Scalable K-Means Clustering

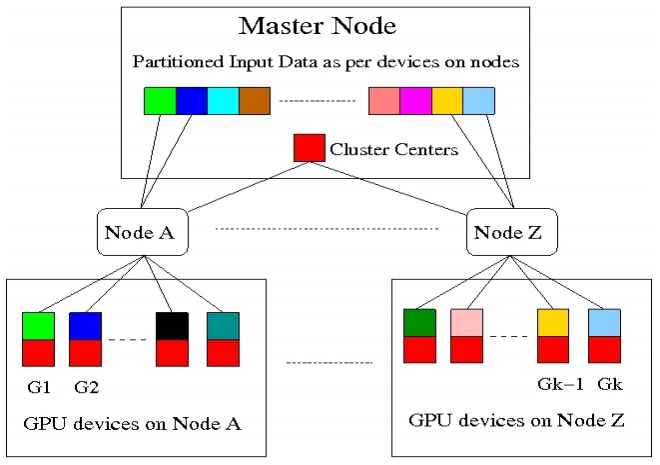K-Means is a popular clustering algorithm with wide applications in Computer Vision, Data mining, Data Visualization, etc. Clustering large numbers of high-dimensional vectors is very computation intensive. In this work, we present the design and implementation of the K-Means clustering algorithm on the modern GPU. A load balanced multi-node, multi-GPU implementation which can handle up to 6 million, 128-dimensional vectors was also developed. Our implementation scales linearly or near-linearly with different problem parameters. We achieve up to 2 times increase in speed compared to the best GPU implementation for K-Means on a single GPU.

4. Error Diffusion Dithering

Many image filtering operations provide ample parallelism, but progressive non-linear processing of images is among the hardest to parallelize due to long, sequential, and non-linear data dependency. A typical example of such an operation is error diffusion dithering, exemplified by the Floyd-Steinberg algorithm. In this work, we present its parallelization on multicore CPUs using a block-based approach and on the GPU using a pixel-based approach. We also develop a hybrid approach in which the CPU and the GPU operate in parallel during the computation. Our implementation can dither an 8K x 8K image on an off-the-shelf laptop with Nvidia 8600M GPU in about 400 milliseconds when the sequential implementation on its CPU took about 4 seconds.

5. Graph Algorithms on CUDA

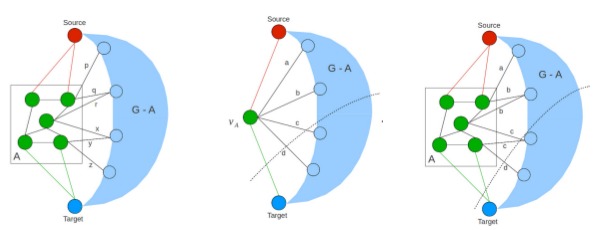We have developed several basic graph algorithms on the CUDA architecture including BFS, Single Source Shortest Path(SSSP), All-Pairs Shortest Path(APSP), and Minimum Spanning Tree computation for large graphs consisting of millions of vertices and edges. We show results on random, scale free and almost linear graphs. Our approaches are 10-50 times faster than their CPU counterparts, on random graphs with an average degree of 6 per vertex.

We have also developed efficient parallel implementations for performing Graph-Cuts on grid graphs in CUDA. Our original work, titled CUDA-Cuts is based on the push-relabel operation for computing the max-flow and hence the min-cut of a graph. We have also developed a multi-resolution framework for max-flow computation which depends on shrink-expand steps in order to solve the graph fully at lower resolution levels, and uses these results to initialize higher resolution graphs closer to convergence. This improves the overall convergence time for the operation.

Related Publications

• Aditya Deshpande and P. J. Narayanan - Can GPUs Sort Strings Efficiently ? Proceedings of the IEEE Conference on High Performance Computing, 18-21 Dec. 2013, Bangalore, India. [PDF]

• Harshit Surekha and P J Narayanan -  Mixed-Resolution Patch-Matching Proceedings of 12th European Conference on Computer Vision, 7-13 Oct. 2012, Vol. ECCV 2012, Part-VI, LNCS 7577, pp. 187-198, Firenze, Italy. [PDF]
  

• Parikshit Sakurikar and P J Narayanan - Fast Graph Cuts using Shrink-Expand Reparameterization Proceedings of IEEE Workshop on Applications of Computer Vision 9-11 Jan. 2012, ISSN 1550-5790 E-ISBN 978-1-4673-0232-6, Print ISBN 978-1-4673-0233-3, pp. 65-71, Breckenridge, CO, USA. [PDF]

• Aditya Deshpande, Ishan Misra and P J Narayanan - Hybrid Implementation of Error Diffusion Dithering Proceedings of 18th International Conference on High Performance Computing 18-21 Dec. 2011, E-ISBN 978-1-4577-1949-3, Print ISBN 978-1-4577-1951-6, pp. 1-10, Bangalore, India. [PDF]

• K. Wasif Mohiuddin and P.J. Narayanan - Scalable Clustering Using Multiple GPUs Proceedings of International Conference on High Performance Computing 18-21 Dec. 2011, E-ISBN 978-1-4577-1949-3, Print ISBN 978-1-4577-1951-6, Bangalore, India. [PDF]
  

• Vibhav Vineet and P. J. Narayanan - CUDA Cuts: Fast Graph Cuts on the GPU Proceedings of CVPR Workshop on Visual Computer Vision on GPUs, 23-28th june, Anchorage, Alaska, USA. IEEE Computer Society 2008 [PDF]

• Pawan Harish and P.J. Narayanan - Accelerating Large Graph Algorithms on the GPU using CUDA Proc of IEEE International Conference on High Performance Computing (HiPC 2007) Goa, December, 2007. [PDF]

Associated People